Last month we attended (virtually) a GPU hackathon hosted by Sheffield and NVIDIA, in order to learn how to create GPU-capable models to accelerate our simulations.
We are working as part of the centre COVID response on models of COVID-19 transmission within the UK. The epidemiologists working on the model are writing stochastic compartmental models where populations are modelled as “Susceptible”, “Exposed”, “Infected”, “Recovered”, etc - movement between these compartments happens stochastically using a set of parameters. The model is a continuous time Markov chain (the next state only depends on the current state) which is solved by splitting each day into four equal time intervals. Parameters themselves are fit in an inference process, which involves running the model many times. The core of this is both “embarrassingly parallel” and has the potential to use over a million threads, and so we wanted to know if we could develop a system that could use the massive parallelism that GPUs might provide.
Our vision (partially achieved) is that one can write R code using the odin domain specific language, and simply add a gpu = TRUE argument, writing
volatility <- odin.dust::odin_dust({
update(x) <- alpha * x + sigma * rnorm(0, 1)
initial(x) <- x0
x0 <- user()
alpha <- user()
sigma <- user()
}, gpu = TRUE)
Provided you have a GPU and appropriate toolchain installed, you will end up with a model that will run in parallel on the GPU:
model <- volatility$new(list(x0 = 0, alpha = 0.91, sigma = 1),
step = 0, n_particles = 100000)
model$run(100)
with the above code creating an instance with 100,000 particles and then running it for 100 steps. This removes from the user a range of problems, from how to safely generate random numbers in parallel through to the details of CUDA programming (which is frankly not terribly pleasant).
We came to the hackathon with an initial proof-of-concept for the above, which could run a simple SIRS (Susceptible-Infected-Recovered-Susceptible) model on both the CPU and GPU. We’re able to use OpenMP within the CPU code to get a linear speedup up to 32 cores (single host) so our aim was to see if we can beat this on a GPU. Our profiling of our full model on the CPU indicated that we were strongly constrained by sampling from the binomial distribution, which took over 50% of our total compute time.
It turns out that this problem is especially bad on a GPU, because the only sensible methods for sampling from the binomial distribution involve rejection sampling. This takes a number of trips through a loop based on random number draws, which is a poor fit for a GPU where you want all your threads ideally doing the same work over and over. By trying to do rejection sampling on a GPU we will get “divergence” where some threads have found their sample, but others are continuing and we’re still waiting on them. In order to stop this being totally distracting we first tried implementing a basic volatility model based on Brownian motion – involving just draws from a normal distribution – we felt this would be a “best case” for our type of stochastic simulation.
With our mentors we started profiling using the relatively new Nvidia tools Nsight compute and Nsight systems, only to find that we had a major problem with lots of small cudaMalloc and cudaMemcpy calls, rather than doing one big one and dividing that up among the threads. This lead to performance that was considerably slower on the GPU than the CPU, and took a day’s refactoring to fix. It also turns out that having lots of small allocations and copies renders the profiler almost unusable, so we could not really begin to optimise our “kernel” (the bit of code we were trying to run on the GPU).
With that sorted out, we explored a variety of optimisations for improving our volatility model, focusing on 8-byte double vs 4-byte float maths (with this making a significant difference on the GPU, whereas I’d always thought of float as essentially an anachronism on the CPU). We found that as we increased the number of particles (independent simulations) and the number of steps that we ran for, the GPU performance increased from being 5x slower than the speed of the CPU to about 150x faster. After this optimisation, it’s likely that most of the metrics here are now measuring the speed at which we can copy data from R, through a C++ layer onto the device, and then reversing this to retrieve the results.
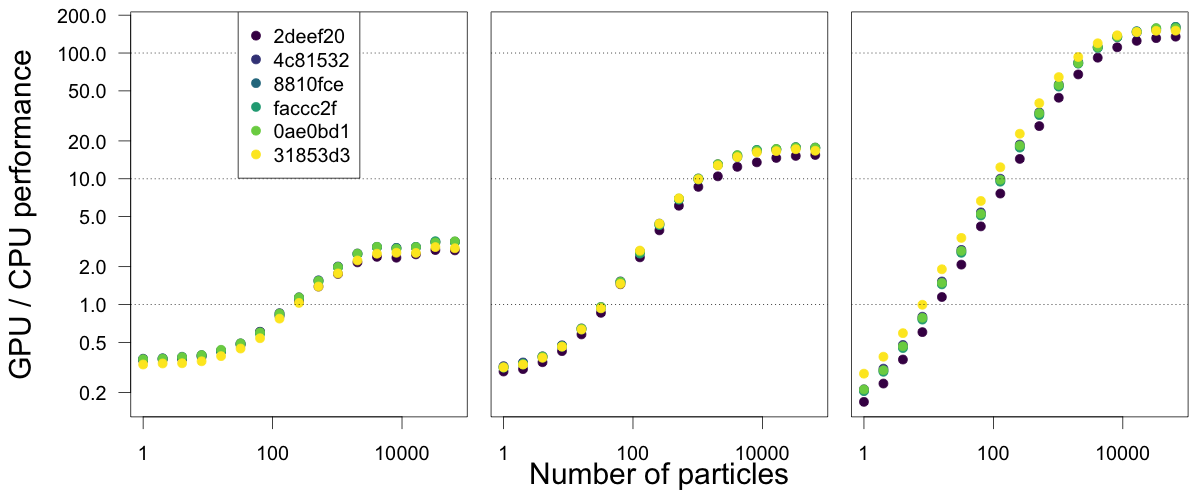
Relative performance of GPU and CPU code for our 'volatlity' model, as we optimised the CUDA code with our mentors - commits are ordered from purple as oldest through to yellow as youngest. The panels run the models for increasing numbers of steps (10, 100, 1000, increasing the time spent on the GPU device relative to the overhead of copying data), and we ran our simulations with 2, 4, 8, ..., 65536 particles, shown on a log scale.
The performance gains here look small, but the kernel itself was sped up by around 10-fold over this process.
Our SIRS model, which relies on samples from a binomial distribution, was more challenging to optimise, though closer to our real model and with more interesting calculations in the kernel. Our initial version was able to run at best 10x faster than the CPU (even after fixing our memory allocations), which we were a bit disappointed in because running the model on a 10-core CPU system is fairly straightforward. For the parameters we were using to start optimising, our kernel was taking ~2s to run, vs 1ms for our optimised version of the volatility model!
With a lot of help from our mentors, and one of the people who has worked on the NVIDIA profiler, we managed to track down the problem. Due to the way we were dealing with divergence we needed to add __syncwarp() to bring threads that have come out of sync due to different numbers of iterations to successfully sample from the binomial distribution. Once we fixed that, our kernel was running in ~40ms and we were much happier. After a few more rounds of optimisation (moving to float rather than double and removing branches that were optimisations in CPU code but caused divergence on the GPU) we ended up with our kernel running in 15ms, a speedup of 130x.
Translated to running our simulation from R, for very large simulations running many steps, we now have GPU performance up to 500x faster than our serial CPU version.
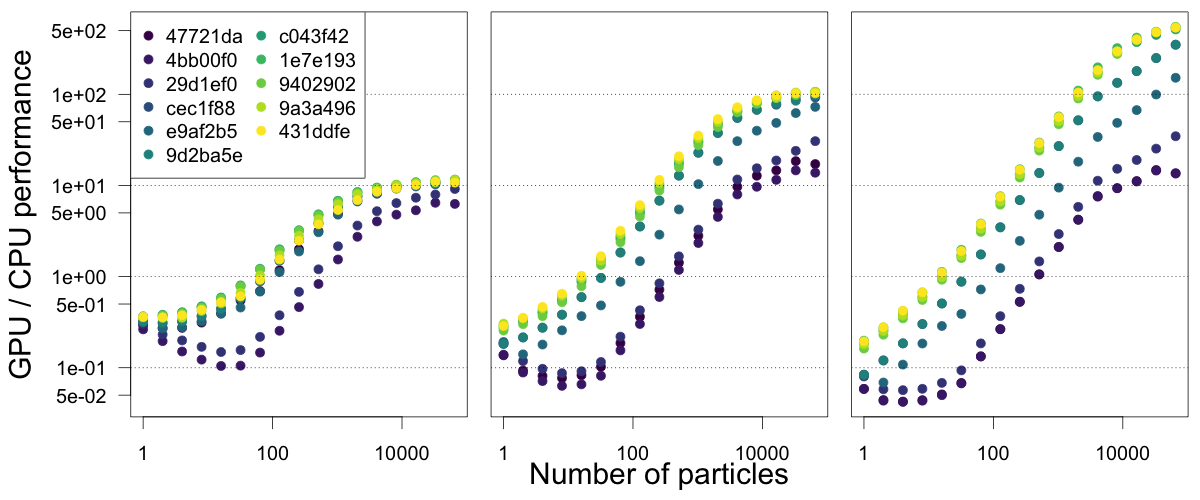
Relative performance of GPU and CPU code for our 'SIRS' model, as we optimised the CUDA code with our mentors - commits are ordered from purple as oldest through to yellow as youngest. The panels run the models for increasing numbers of steps (10, 100, 1000, increasing the time spent on the GPU device relative to the overhead of copying data), and we ran our simulations with 2, 4, 8, ..., 65536 particles, shown on a log scale.
There’s a large gap between our toy models and our real system, and it’s not entirely clear how our performance will translate. Our real model has many binomial draws within a step, and will do relatively large amounts of computation within a run before passing results back to R, so it’s possible that it will be good. On the other hand, more variation in the parameters to the binomial random draws may increase the amount of divergence and we’ll lose out. Unfortunately, to run our real model we need to refactor how our GPU implementation holds internal state, so it will be a while before we know.
Where to next? We have a pretty good sense of the problems blocking running our full model on the GPU and will work over the coming months to remove this. We’re not convinced that this will definitely be worthwhile for models that rely heavily on binomial random numbers and other discrete distributions (Poisson, hypergeometric, etc) but for models that involve incorporating Brownian motion our approach might provide a very high level approach to implement models that can be run massively in parallel.
Our current implementation is only a proof-of-concept, and languishes on a branch for the time being, however over the winter we plan on converting this into a fully working system.
We’re very grateful to our mentors Paul Richmond and Rob Chisholm, both of the Sheffield RSE group for helping us understand the issues in our model and optimising it, along with all the organisers of the hackathon!